: Catalanova čísla
Prezentace (pdf)
Zadání
Najděte a popiště bijekci mezi následujícími dvěma množinami:
- množina všech Dyckových cest délky neboli všech cest z bodu do bodu za použití kroků nahoru a kroků dolů , které nikdy neklesnou pod osu ;
- množina všech celých binárních stromů s vnitřními vrcholy, kde každý vnitřní vrchol má právě dva potomky.
Příklad:
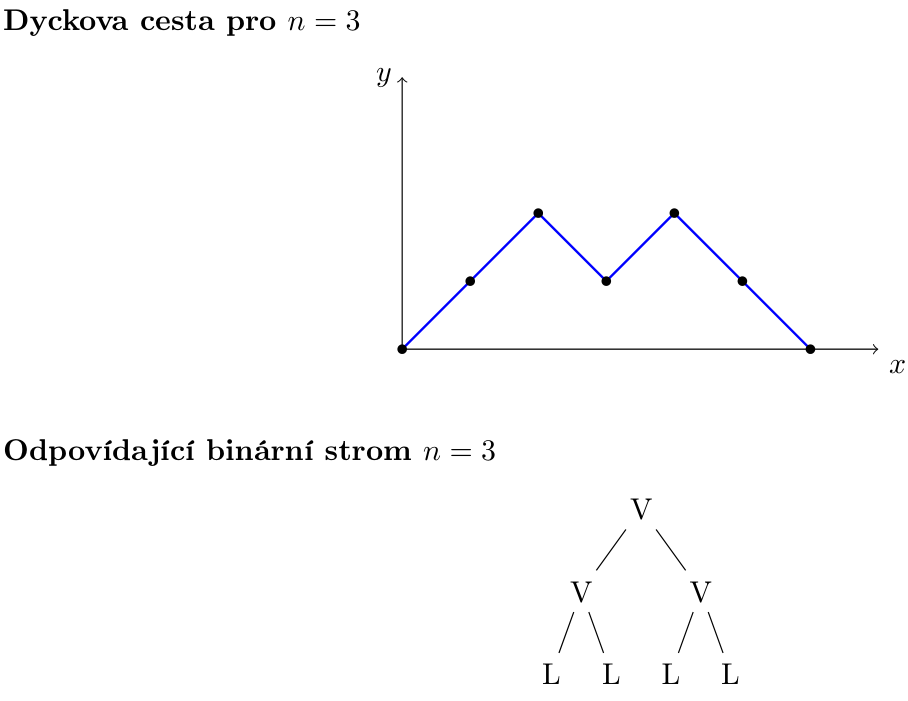
Řešení od autora
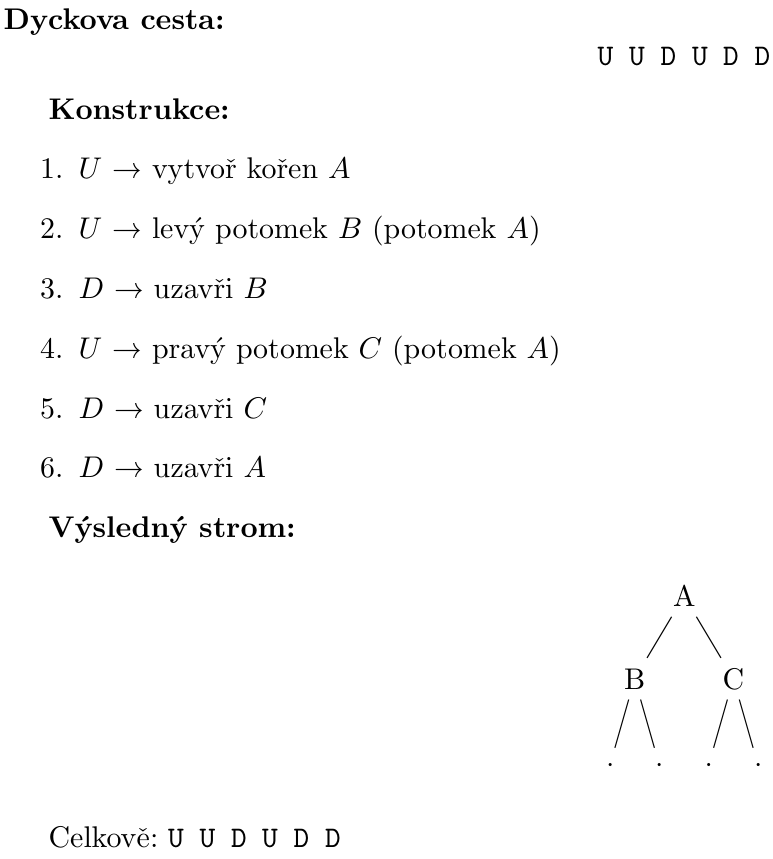
Zapíšeme Dyckovu cestu ve tvaru a potom tvoříme strom následovně:
- První znamená: vytvoř kořen stromu.
- Každý další krok znamená: vytvoř nový vnitřní uzel nalevo (pokud nalevo už je, vytvoř napravo) od předešlého a sestup do něj.
- Každý další krok znamená: dokonči uzel (dodělej mu listy tak, aby měl dva potomky) a vrať se o úroveň výše (k předkovi).
Příklad: